¿Por qué no dividimos por cero?
contenido
Los lectores pueden preguntarse por qué dedico un artículo completo a un tema tan banal. La razón es la asombrosa cantidad de estudiantes (!) que casualmente llevan a cabo la operación bajo el nombre. Y no solo estudiantes. A veces cojo y profesores. ¿Qué podrán hacer en matemáticas los alumnos de tales profesores? El motivo inmediato para escribir este texto fue una conversación con un profesor para quien la división por cero no era un problema...
Con cero, sí, excepto por la molestia de nada en absoluto, porque realmente no necesitamos usarlo en la vida cotidiana. No vamos de compras por cero huevos. "Hay una persona en la habitación" suena algo natural, y "cero personas" suena artificial. Los lingüistas dicen que el cero está fuera del sistema lingüístico.
También podemos prescindir del cero en las cuentas bancarias: simplemente use, como en un termómetro, rojo y azul para valores positivos y negativos (tenga en cuenta que para la temperatura es natural usar rojo para números positivos, y para cuentas bancarias es es al revés, porque el débito debería activar una advertencia, por lo que se recomienda encarecidamente el rojo).
Al incluir el cero como número natural, tocamos el problema de la diferenciación Numeros cardinales od familiar. Dentro de 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..
la potencia del número es igual al número del lugar donde se encuentra. De lo contrario, ya está en la secuencia 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …..
El número de conjuntos singleton ocupa el segundo lugar, el número de conjuntos con dos elementos ocupa el tercer lugar, y así sucesivamente. Tenemos que explicar por qué, por ejemplo, no numeramos los lugares de los atletas en las competencias desde cero. Luego, el ganador del primer lugar recibiría una medalla de plata (el oro fue para el ganador del lugar cero), y así sucesivamente. En el fútbol se usó un procedimiento algo similar: no sé si los lectores saben que "liga uno" significa " siguiendo a los mejores". “, y la liga cero está llamada a convertirse en la “liga mayor”.
A veces escuchamos el argumento de que debemos comenzar desde cero, porque es conveniente para la gente de TI. Continuando con estas consideraciones, se debe cambiar la definición de un kilómetro: debe ser 1024 m, porque esta es la cantidad de bytes en un kilobyte (me referiré a una broma conocida por los informáticos: "¿Cuál es la diferencia entre un estudiante de primer año y un estudiante de informática y un estudiante de quinto año de esta facultad? que un kilobyte son 1000 kilobytes, el último - que un kilómetro son 1024 metros")!
Otro punto de vista, que ya debería tomarse en serio, es este: ¡siempre medimos desde cero! Es suficiente mirar cualquier escala en la regla, en las escalas domésticas, incluso en el reloj. Dado que medimos desde cero, y contar puede entenderse como una medida con una unidad adimensional, entonces deberíamos contar desde cero.
Es un asunto sencillo, pero...
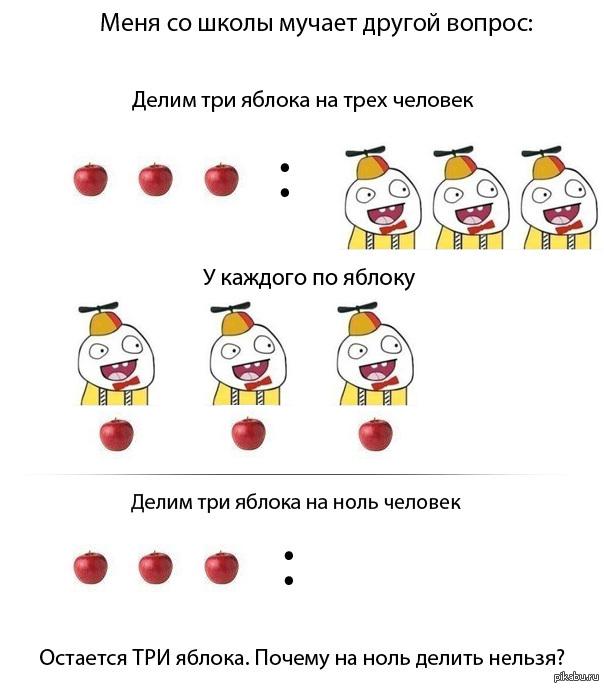
Dejemos el razonamiento general y volvamos a la división por cero. El asunto es sencillo y sería sencillo si no fuera por... ¿y qué? Pensemos e intentemos. ¿Cuánto puede ser - uno dividido por cero? Veamos: 1/0 = x. Multiplica ambos lados por el denominador del lado izquierdo.
Obtenemos 1=0. ¡Algo está mal! ¿Qué sucedió? ¡Adivina! La suposición de que hay un cociente de la unidad y cero conduce a una contradicción. Y si uno no se puede dividir por cero, otro número sí. Si, lector, te encoges de hombros y te preguntas por qué el autor (es decir, yo) escribe sobre tales lugares comunes, entonces ... ¡Estoy muy contento!
La fórmula 0/0 = 0 podría defenderse de manera obstinada, pero contradice la regla de que el resultado de dividir un número por sí mismo es igual a uno. Absolutamente, pero muy diferentes son símbolos como 0/0, °/° y similares en cálculo. No significan ningún número, sino que son designaciones simbólicas para secuencias particulares de ciertos tipos.
En un libro de ingeniería eléctrica, encontré una comparación interesante: dividir por cero es tan peligroso como la electricidad de alto voltaje. Esto es normal: la ley de Ohm establece que la relación entre el voltaje y la resistencia es igual a la corriente: V = U / R. Si la resistencia fuera cero, una corriente teóricamente infinita fluiría a través del conductor, quemando todos los conductores posibles.
Una vez escribí un poema sobre los peligros de dividir por cero todos los días de la semana. Recuerdo que el día más dramático fue el jueves, pero es una pena por todo mi trabajo en esta área.
Cuando divides algo por cero
Lunes muy temprano
Semana lo que acaba de pasar
Ya has fallado miserablemente.
cuando el martes por la tarde
pones cero en el denominador
Te diré entonces, te equivocas
¡Mal matemático!
Cuando a través del cero, a través de la perversión,
Quiero separarme el miércoles
Te meterás en muchos problemas
¡Tienes heno y agua en la cabeza!
Un tal Bartek estaba con nosotros.
Estaba en desacuerdo con las reglas.
El jueves, es divisible por cero.
¡Él ya no está entre nosotros!
Si un extraño deseo se apodera de ti
Dividir por cero el viernes
Seré honesto, seré honesto:
Mal comienzo de este fin de semana.
Cuando es cero, en algún lugar el sábado
El divisor será tuyo (sin negrita)
Arrodíllate debajo de la cerca de la iglesia.
Esta es tu resurrección.
¿Quieres cero debajo del tablero,
Hacer un día de fiesta el domingo
Traiga tiza, pizarra negra.
Escribe: ¡no es divisible por cero!
El cero está asociado con el vacío y la nada. De hecho, llegó a las matemáticas como una cantidad que, cuando se suma a alguna, no la cambia: x + 0 = x. Pero ahora cero aparece en varios otros valores, más notablemente como inicio de escala. Si fuera de la ventana no hay temperatura positiva ni escarcha, entonces ... esto es cero, lo que no significa que no haya temperatura en absoluto. Un monumento de clase cero no es uno que lleva mucho tiempo demolido y simplemente no existe. Al contrario, es algo así como el Wawel, la Torre Eiffel y la Estatua de la Libertad.
Bueno, la importancia del cero en un sistema posicional difícilmente puede sobreestimarse. ¿Sabes, lector, cuántos ceros tiene Bill Gates en su cuenta bancaria? No sé, pero me gustaría la mitad. Aparentemente, Napoleón Bonaparte notó que las personas son como ceros: adquieren significado a través de la posición. En la película de Andrzej Wajda As the Years, As the Days Go by, el apasionado artista Jerzy explota: "El filisteo es cero, nihil, nada, nada, nihil, cero". Pero cero puede ser bueno: “desviación cero de la norma” significa que todo va bien, ¡y sigue así!
Volvamos a las matemáticas. El cero se puede sumar, restar y multiplicar con total impunidad. “Gané cero kilogramos”, le dice Manya a Anya. “Y esto es interesante, porque perdí el mismo peso”, responde Anya. Así que comamos seis cero porciones de helado seis veces, no nos hará daño.
No podemos dividir por cero, pero podemos dividir por cero. Un plato de bolas de masa cero se puede entregar fácilmente a aquellos que esperan comida. ¿Cuánto recibirá cada uno?
El cero no es positivo ni negativo. este y el numero no positivoи no negativo. Satisface las desigualdades x≥0 y x≤0. La contradicción "algo positivo" no es "algo negativo", sino "algo negativo o igual a cero". Los matemáticos, contrariamente a las reglas del lenguaje, siempre dirán que algo es "igual a cero" y no "cero". Para justificar esta práctica tenemos: si leemos la fórmula x = 0 "x es igual a cero" entonces x = 1 leemos "x es igual a uno", que podría tragarse, pero ¿qué pasa con "x = 1534267"? ? Tampoco puede asignar un valor numérico al carácter 00ni elevar el cero a una potencia negativa. Por otro lado, puedes rootear cero a voluntad... y el resultado siempre será cero.
Función exponencial y = ax, la base positiva de a, nunca se convierte en cero. De ello se deduce que no hay logaritmo cero. En efecto, el logaritmo de a en base b es el exponente al que debe elevarse la base para obtener el logaritmo de a. Para a = 0, no existe tal indicador y cero no puede ser la base del logaritmo. Sin embargo, el cero en el "denominador" del símbolo de Newton es otra cosa. Suponemos que estas convenciones no conducen a una contradicción.
evidencia falsa
La división por cero es un tema común para las pruebas falsas, y les sucede incluso a matemáticos experimentados. Déjame darte dos de mis ejemplos favoritos. La primera es algebraica. Voy a "probar" que todos los números son iguales. Supongamos que hay dos números que no son iguales. Por tanto, uno de ellos es mayor que el otro, sea a > b. Supongamos que c es su diferencia
c \uXNUMXd a - b. Entonces tenemos a - b = c, de donde a = b + c.
Multiplicamos ambas partes de este último por a - b:
a2 – ab = ab + ca – b2 – antes de Cristo.
Traduzco ak al lado izquierdo, por supuesto que recuerdo haber cambiado el signo:
a2 - ab - ac = ab - b2 - bc.
Excluyo factores comunes:
A (a-b-c) \uXNUMXd b (a-b-c),
Comparto y tengo lo que queria:
a = b.
Y en realidad aún más extraño, porque supuse que a > b, y obtuve que a = b. Si en el ejemplo anterior "hacer trampa" es fácil de reconocer, entonces en la siguiente prueba geométrica no es tan fácil. Probaré que... el trapezoide no existe. La figura comúnmente llamada trapezoide no existe.
Pero supongamos primero que existe un trapezoide (ABCD en la figura siguiente). Tiene dos lados paralelos ("bases"). Estiramos estas bases, como se muestra en la imagen, para obtener un paralelogramo. Sus diagonales dividen la otra diagonal del trapezoide en segmentos cuyas longitudes se denotan x, y, z, como en figura 1. De la semejanza de los triángulos correspondientes, obtenemos las proporciones:
donde definimos:
Oraz
donde definimos:
Resta los lados de igualdad marcados con asteriscos:
Acortando ambos lados por x − z, obtenemos – a/b = 1, lo que significa que a + b = 0. Pero los números a, b son las longitudes de las bases del trapezoide. Si su suma es cero, entonces también son cero. ¡Esto significa que una figura como un trapezoide no puede existir! Y como los rectángulos, los rombos y los cuadrados también son trapezoides, entonces, querido lector, tampoco existen los rombos, los rectángulos y los cuadrados...
Adivina Adivina
Compartir información es la más interesante y desafiante de las cuatro actividades básicas. Aquí, por primera vez, nos encontramos con un fenómeno tan común en la edad adulta: "adivina la respuesta y luego comprueba si acertaste". Esto lo expresa muy acertadamente Daniel K. Dennett (“¿Cómo cometer errores?”, en How It Is – A Scientific Guide to the Universe, CiS, Varsovia, 1997):
Este método de "adivinar" no interfiere con nuestra vida adulta, quizás porque lo aprendemos temprano y adivinar no es difícil. Ideológicamente, el mismo fenómeno ocurre, por ejemplo, en la inducción matemática (completa). En el mismo lugar, "adivinamos" la fórmula y luego verificamos si nuestra suposición es correcta. Los estudiantes siempre preguntan: “¿Cómo supimos el patrón? ¿Cómo se puede sacar?" Cuando los estudiantes me hacen esta pregunta, la convierto en una broma: "Lo sé porque soy un profesional, porque me pagan por saber". Se puede responder a los estudiantes en la escuela con el mismo estilo, solo que con más seriedad.
ejercicio. Tenga en cuenta que comenzamos la suma y la multiplicación escrita con la unidad más baja y la división con la unidad más alta.
Una combinación de dos ideas.
Los profesores de matemáticas siempre han señalado que lo que llamamos separación adulta es la unión de dos ideas conceptualmente diferentes: viviendas i separación.
El primero (viviendas) ocurre en tareas donde el arquetipo es:
dividir-dividir Son tareas como:
? (Conservamos el estilo original de este problema, tomado del manual de Julian Zgozalewicz publicado en Cracovia en 1892 - el złoty es el złoty renano, la moneda que estuvo en circulación en el Imperio Austro-Húngaro hasta principios del siglo XIX).
Ahora considere dos problemas con el libro de texto de matemáticas más antiguo en polaco, padre Tomasz Clos (1538). ¿Es una división o un cupé? Resolverlo como deberían hacerlo los escolares del siglo XIX:
(Traducción del polaco al polaco: Hay un cuarto y cuatro ollas en un barril. Una olla son cuatro cuartos. Alguien compró 20 barriles de vino por 50 zł para comerciar. Los aranceles e impuestos (¿impuestos especiales?) serán 8 zł. ¿Cuánto pagar? vender un cuarto para ganar 8 zł?)
Deportes, física, congruencia
A veces en los deportes hay que dividir algo por cero (proporción de goles). Bueno, los jueces de alguna manera se ocupan de eso. Sin embargo, en álgebra abstracta están a la orden del día. cantidades distintas de cerocuyo cuadrado es cero. Incluso se puede explicar de forma sencilla.
Considere una función F que asocia un punto (y, 0) con un punto en el plano (x, y). que es f2, es decir, una doble ejecución de F? Función cero: cada punto tiene una imagen (0,0).
Finalmente, las cantidades distintas de cero cuyo cuadrado es 0 son casi el pan de cada día para los físicos, y los números de la forma a + bε, donde ε ≠ 0, pero ε2 = 0, los matemáticos llaman números dobles. Ocurren en el análisis matemático y en la geometría diferencial.
Después de todo, hay algo en aritmética que tiene división por cero al menos en el nombre. Viene de congruencia. Sea Z el conjunto de enteros. Dividir el conjunto Z por p significa que igualamos cada número (entero) a algunos otros, es decir, a aquellos por los que su diferencia es divisible. Entonces, cuando tenemos cinco tipos de números correspondientes a los números 0, 1, 2, 3, 4, los posibles restos cuando se dividen por 5. La fórmula se escribe así:
mod cuando la diferencia es un múltiplo.
Para = 2, solo tenemos dos números: 0 y 1. Dividir números enteros en dos clases de este tipo equivale a dividirlos en pares e impares. Vamos a reemplazarlo ahora. La diferencia siempre es divisible por 1 (cualquier número entero es divisible por 1). ¿Es posible tomar =0? Intentemos: ¿cuándo la diferencia de dos números es un múltiplo de cero? Sólo cuando estos dos números son iguales. Entonces, dividir un conjunto de números enteros por cero tiene sentido, pero no es interesante: no pasa nada. Sin embargo, se debe enfatizar que esto no es una división de números en el sentido conocido desde la escuela primaria.
Tales acciones están simplemente prohibidas, así como las matemáticas largas y amplias.
Arroz. 2. Identificación de números mediante comparación
(modo 5 y modo 2)

